分數量子反常霍爾效應(FQAHE)是零磁場下分數量子霍爾效應的拓撲類比,其實現依賴于時間反演對稱性破缺的平坦能帶,并可能催生非阿貝爾任意子——拓撲量子計算的核心載體。此前,FQAHE僅在扭曲MoTe?(v > 1/2)中被觀測到,而基于石墨烯的摩爾超晶格因高遷移率和低缺陷潛力備受關注,但長期未實現FQAHE突破。
本研究首次在菱形五層石墨烯-六方氮化硼(hBN)摩爾超晶格中觀測到零磁場下的整數量子反常霍爾效應(IQAHE)和FQAHE。在摩爾填充因子v=1時,霍爾電阻R_xy呈現量子化平臺±h/e²(對應陳數C=±1);在0<v<1范圍內,發現六個分數量子化平臺(v=2/3、3/5、4/7、4/9、3/7、2/5),R_xy=h/(νe²)且縱向電阻R_xx顯著下降。v=1/2時R_xy=h/2e²隨v線性變化,類似復合費米液體(CFL)行為。通過調控柵極位移場D和v,實驗揭示了從CFL、FQAH態到谷極化費米液體及相關絕緣體的動態相變。
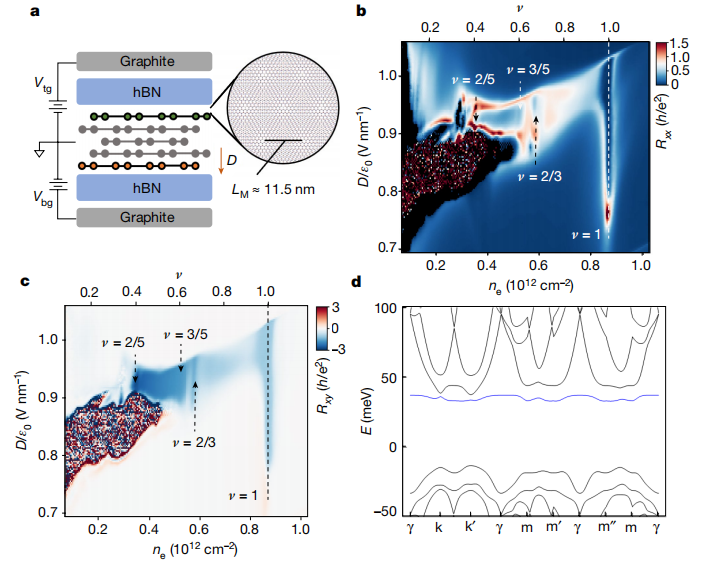
圖1 | 菱形五層石墨烯-hBN摩爾超晶格的器件結構、拓撲平帶及相圖
a,器件結構示意圖,展示了石墨烯頂層與頂部hBN之間形成的摩爾超晶格,其周期為11.5納米。
b-c,通過對稱化縱向電阻Rxx(b)和反對稱化橫向電阻Rxy(c)在磁場B=±0.1 T下揭示的器件相圖,作為載流子密度ne(v)和柵極位移場D的函數。稀釋制冷機混合腔溫度為10毫開爾文。在D/ε?≈0.93伏特/納米為中心區域的傾斜帶狀區域內,觀察到顯著的反常霍爾信號。在摩爾超晶格填充因子v=1、2/3、3/5和2/5處(由虛線和箭頭標出),Rxx呈現明顯凹陷,同時Rxy顯示出量子化平臺。
d,通過層間電勢差Δ=75毫電子伏特計算的摩爾超晶格能帶結構,顯示出一個平坦的|C|=1摩爾導帶和一個色散的C=0摩爾價帶。
(注:ε?為真空介電常數,C為陳數,描述能帶的拓撲性質。)
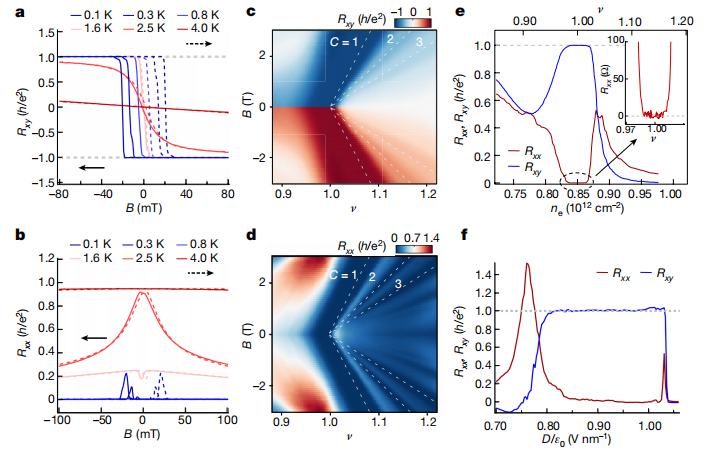
圖2 | 整數量子反常霍爾效應(IQAHE)
a,b,在填充因子v=1、位移場D/ε?=0.97伏特/納米及溫度T=0.1–4開爾文條件下,橫向電阻Rxy(a)和縱向電阻Rxx(b)的磁滯回線掃描。實線(虛線)對應磁場B從正值(負值)向負值(正值)掃描。在0.1開爾文時,Rxy量子化于±h/e²,對應陳數C=±1;而Rxx在零磁場(B=0毫特斯拉)下的值低于5歐姆。
c,d,D/ε?=0.97伏特/納米時,Rxy(c)和Rxx(d)的朗道扇圖。整數量子反常霍爾態在兩張圖中均表現為寬平臺,其隨磁場變化的斜率與虛線(基于Streda公式確定的C=±1)高度吻合。當磁場超過約0.6特斯拉時,對應于C=±2和3的整數量子霍爾態開始出現(由附加虛線標出)。
e,在T=10毫開爾文和D/ε?=0.97伏特/納米條件下,對稱化Rxx和反對稱化Rxy(為方便顯示取正值)隨填充因子v的變化曲線。Rxy在約3×10¹?厘米?²的寬平臺內量子化,插圖為局部放大圖,顯示Rxx<5歐姆的平臺區域。
f,固定v=1時,Rxx和Rxy隨位移場D的變化曲線。在D≈0.8–1.03伏特/納米范圍內,器件呈現寬平臺特征;當D向更高或更低值偏離時,系統轉變為Rxx和Rxy較小的金屬態,并在相變過程中出現Rxx峰值。
(注:ε?為真空介電常數,朗道扇圖用于描述量子霍爾態隨磁場和載流子密度的演化,Streda公式關聯陳數與霍爾電導。)
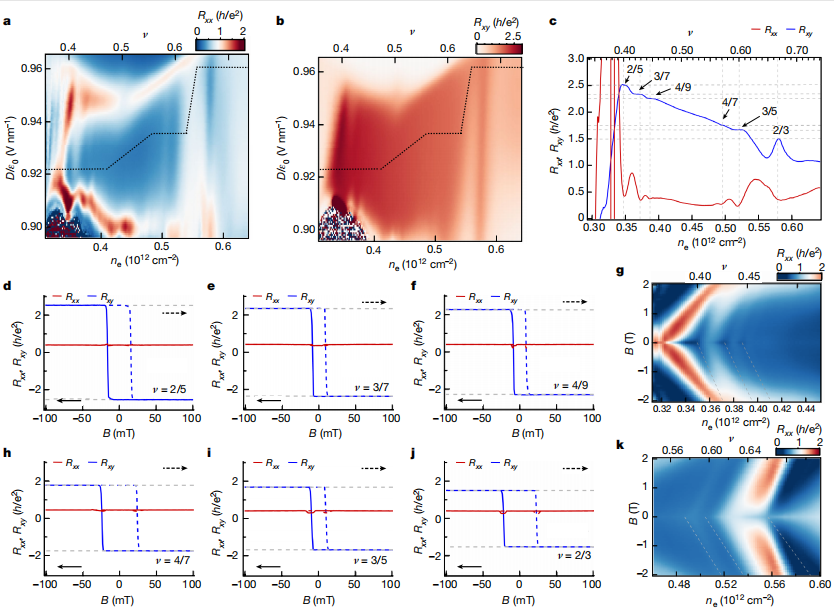
圖3 | 分數量子反常霍爾效應(FQAHEs)
a-b,在磁場B=±0.1 T下,對稱化縱向電阻Rxx(a)和反對稱化橫向電阻Rxy(b)(為方便顯示取正值)隨填充因子v(載流子密度ne)及位移場D變化的局部放大圖。在v=1/2附近(尤其是Rxx圖中),可觀察到圖1d-e中未分辨的精細特征。數據通過恒壓偏置法測量。
c,沿a和b中虛線路徑的Rxx和Rxy(恒流法測量)。在v=2/5、3/7、4/9、4/7、3/5和2/3處(由虛線和箭頭標出),Rxy呈現清晰的量子化平臺:5h/(2e²)、7h/(3e²)、9h/(4e²)、7h/(4e²)、5h/(3e²)和3h/(2e²),對應Rxx在相同填充因子處顯著凹陷。
d-f, h-j,v=2/5(d)、3/7(e)、4/9(f)、4/7(h)、3/5(i)和2/3(j)時Rxy和Rxx的磁滯回線掃描,顯示Rxy量子化為h/(νe²),且Rxx顯著降低。
g, k,D/ε?=0.92伏特/納米時的Rxx朗道扇圖。FQAH態表現為傾斜的線狀特征,其斜率與虛線(基于Streda公式計算的陳數C=2/5、3/7、4/9(g)及C=4/7、3/5、2/3(k))高度吻合。
(注:Streda公式將霍爾電導與陳數關聯,分數陳數對應分數量子化霍爾平臺。)
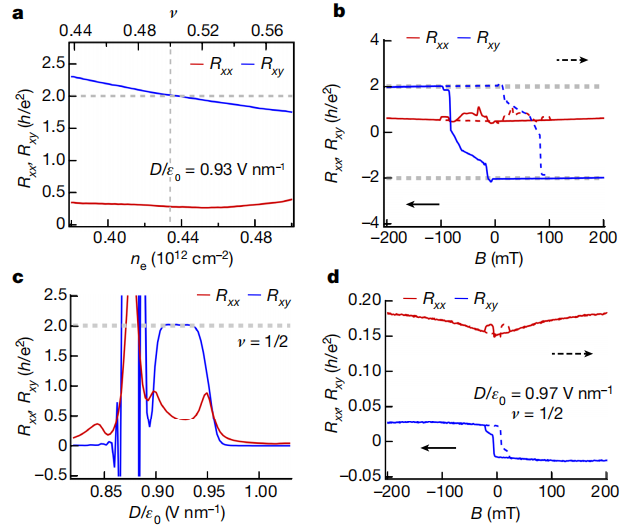
圖4 | 半填充時的反常霍爾效應及相變
a,在磁場B=±0.1 T、位移場D/ε?=0.93伏特/納米條件下,半填充(v=1/2)附近的對稱化縱向電阻Rxx和反對稱化橫向電阻Rxy(為方便顯示取正值)。Rxy在v=1/2處呈現2h/e²的量子化值(對應陳數C=2),并隨填充因子近似線性變化,而Rxx未出現顯著凹陷。此行為與強磁場下二維電子氣(2DEG)中復合費米液體(CFL)的特征相似。
b,v=1/2時Rxy和Rxx的磁滯回線掃描,顯示Rxy穩定于±2h/e²平臺且Rxx極小。
c,固定v=1/2時,Rxy和Rxx隨位移場D的變化曲線。在D=0.9–0.94伏特/納米范圍內,Rxy保持量子化平臺;當D更高時,Rxy和Rxx均趨近于零;當D更低時,Rxx急劇上升,Rxy則圍繞零值劇烈波動。
d,在v=1/2、D/ε?=0.97伏特/納米條件下的Rxy和Rxx磁滯回線掃描,顯示反常霍爾信號及霍爾角θ_H≈9.5°(對應tanθ_H≈Rxy/Rxx≈0.17)。這表明在更高D側,系統從CFL相轉變為谷極化金屬;而在更低D側,CFL與關聯絕緣態之間發生相變。
(注:CFL為復合費米液體,θ_H為霍爾角,ε?為真空介電常數;陳數C=2對應霍爾電導σ_xy=2e²/h。)
該系統的獨特優勢在于:
材料創新性:五層石墨烯-hBN超晶格未經過往理論預測,卻展現出豐富量子態;
零磁場操控:為研究電荷分數化、非阿貝爾編織提供理想平臺;
多參數可調性:通過層數、位移場、扭曲角優化,可探索更高陳數能帶及奇異FQAH態;
超導-FQAHE共存潛力:未來或通過側向結實現非阿貝爾任意子合成。
這一發現不僅拓展了FQAHE的材料體系,更為拓撲量子計算和強關聯電子物理開辟了新路徑。后續研究可聚焦于零磁場電子晶體、新型量子相變及高陳數能帶的實驗驗證,推動石墨烯基量子器件的實用化進程。
轉自《石墨烯研究》公眾號